Inverse system
In mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.
Contents |
The category of inverse systems
Pro-objects in C form a category pro-C. Two inverse systems
- F:I
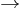C
and
G:J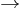 C determine a functor
- Iop x J 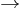Sets,
namely the functor
.
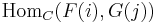The set of homomorphisms between F and G in pro-C is defined to be the colimit of this functor in the first variable, followed by the limit in the second variable.
If C has all inverse limits, then the limit defines a functor pro-C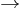C. In practice, e.g. if C is a category of algebraic or topological objects, this functor is not an equivalence of categories.
Direct systems/Ind-objects
An ind-object in C is a pro-object in Cop. The category of ind-objects is written ind-C.
Examples
- If C is the category of finite groups, then pro-C is equivalent to the category of profinite groups and continuous homomorphisms between them.
- If C is the category of finitely generated groups, then ind-C is equivalent to the category of all groups.
References
- Bourbaki, Nicolas (1968), Elements of mathematics. Theory of sets, Translated from the French, Paris: Hermann, MR0237342.
- Hazewinkel, Michiel, ed. (2001), "Inverse system", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=S/s091930